알고리즘 문제를 풀면서 반드시 알아야 할 알고리즘 중 하나는 아마 재귀 알고리즘일거라 생각합니다. 재귀 함수를 사용할 수 있는 곳에서는 재귀 함수를 사용하며 알고리즘을 풀면서 공부를 해야 된답니다.

재귀 함수

재귀 함수는 함수내에서 다시 자신을 호출한 후 그 함수가 끝날때까지 함수 호출 이후의 명령문을 수행하지 않습니다. 즉, “반복문 + 스택구조가 결합된 함수를 재귀함수라고 볼 수 있습니다. 스택 구조가 결합된 함수에 대해서 조금 더 풀어서 이야기해보도록 하겠습니다. 스택구조가 결합되었다는 의미는 먼저 들어간 데이터가 가장 마지막에 나오는 구조, 나중에 들어간 데이터가 가장 먼저 나오는 구조(후입선출) 을 말합니다.

쉬운 예를 들어보겠습니다.

def hap(a,b):
    print(a+b)

def gop(a,b):
    print(a*b)

def hap_gop(a,b):
    hap(a,b)
    gop(a,b)

print(hap_gop(7,8))

hap_gop함수는 그냥 a와 b값을 받아서 hap 함수와 gop함수에 던져주는 역할만 수행합니다. hap_gop함수가 hap함수와 gop함수를 호출(다른 함수)한다는 뜻이죠. 그런데, “재귀함수는 자기 자신의 함수를 호출한다” 라는 특징이 있습니다.

def countdown(n):
    if n == 0:
        print('발사')
    else:
        print(n)
        countdown(n-1)   # 자기 자신을 호출 !

print(countdown(5))

더 쉬운 예로 위의 함수와 똑같이 구현하여 구구단 2단을 출력해보도록 하겠습니다.

def tow_count(n):
  if n != 0:
      print('2 x %d = %d' %(n,2*n))
      tow_count(n-1)

tow_count(10)

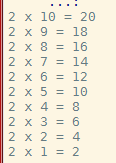
위와 같이 결과가 나왔을 때, 다시 2 x 1 = 2 … 로 출력하려면 어떻게 해야댈까요 ?
재귀 함수를 이용하면 쉽게 구현할 수 있습니다. 아까 말했던 것 처럼 스택구조가 결합된 함수이기 때문에 먼저 들어간 데이터가 가장 마지막에 나오는 구조라고 했습니다. 그래서 아래와 같이 재귀함수를 구현하여 출력할 수 있습니다.

def tow_count(n):
  if n != 0:
      tow_count(n-1)
      print(('2 x %d = %d') %(n,2*n))

tow_count(10)

구구단이 제대로 출력되는 모습을 볼 수 있습니다.

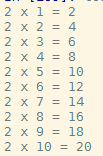
즉, 재귀는 숫자를 0까지 계속 waiting 시켰다가 나가는 스택구조를 띄고 있다는 것을 알수 있습니다.