신경망이라는 것을 접하면서 미분, 기울기와 같은 말을 몇번 들어봤다.
우리는 왜 미분을 사용하는 것인지, 미분이 필요한 이유와 도함수를 Python 으로 간단하게 구현해보도록 하겠다.

미분이 필요한 이유

미분이 필요한 이유는 기존의 가중치를 갱신하기 위해서 사용한다.
하지만 진정한 미분은 컴퓨터로 구현하기 어렵기 때문에 중앙 차분 오차가 발생한다. 그래서 컴퓨터로 미분을 구현하기 위해서는 수치 미분을 사용해야한다.

함수 y=f(x)에 대해서 x가 x_{0} 에서 x_{0}+h 로 변화할 때, y의 값은 f(x_{0}+h)로 변화한다고 할 때, 평균 변화율은 아래와 같다

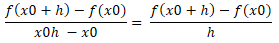
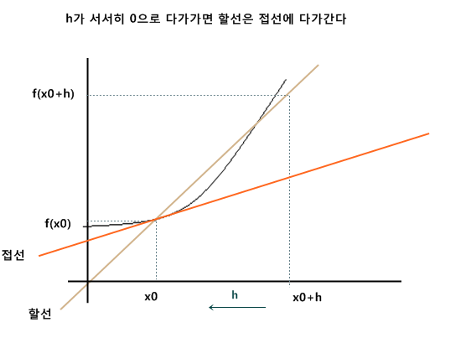
그림을 보면 h가 서서히 0으로 다가가면 할선은 접선으로 다가간다.

이를 코드로 구현하려면 h가 되었을때가 진정한 미분이라고 할수 있는데, 아까 말했던 것과 같이 컴퓨터로는 진정한 미분을 구현하는 것은 어렵다.
h가 0이 될 수 없기 때문이며, 그래서 h를 0.0001로 두고 수치미분을 한다.

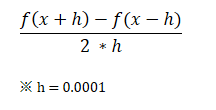
수치 미분

함수 이름은 numerical_diff 라고 짓었다. 위의 공식을 보고 그대로 만들면 되기 때문에 간단하게 함수를 구현할 수 있다.

def numerical_diff(f,x):
    h=0.001
    return (f(x+h)-f(x-h)) / (2*h)

위의 미분 함수를 이용하여 f(x)=x^2 + 4^2 함수를 미분하고 x=4에서의 미분계수(기울기)를 구하면, 2x + 0 상수는 도함수가 되면 0이 되고, 2*4 = 8 이 된다.

def samplefunc1(x):
    return x**2 + 4**2

print(numerical_diff(samplefunc1,4))

결과 값을 출력하면 8이 나오지 않고 근사치가 나오는 것은 수치미분이기 때문에 중앙 차분 오차가 발생하기 때문이다.

import numpy as np
import matplotlib.pylab as plt

def samplefunc1(x):
    return x**2 + 4**2

x = np.arange(0.0, 20.0, 0.1) 
y = samplefunc1(x)
plt.plot(x,y)
plt.show()

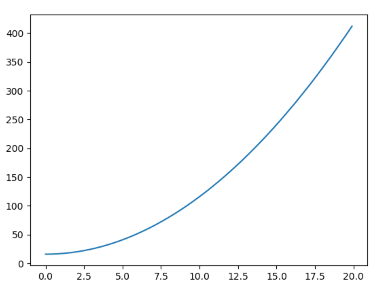
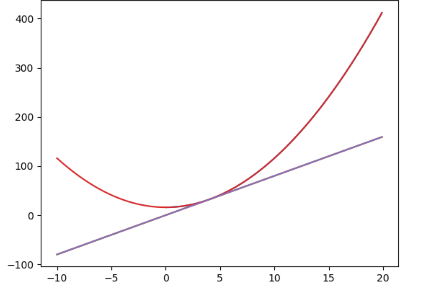
여기에 도함수 그래프를 넣어 겹쳐서 보려고 한다.

import numpy as np
import matplotlib.pylab as plt

def numerical_diff(f,x):
    h=0.001
    return (f(x+h)-f(x-h)) / (2*h)

def samplefunc1(x):
    return x**2 + 4**2

def afterfunc(x):
    return numerical_diff(samplefunc1,4)*x

x1 = np.arange(-10.0, 20.0, 0.1) 
y1 = samplefunc1(x1)
plt.plot(x1,y1)

x2= np.arange(-10.0, 20.0, 0.1) 
y2 = afterfunc(x2)
plt.plot(x2,y2)

plt.show()