머신러닝에서 활성화 함수란?(Activation function)

이번 포스팅에서는 활성화 함수가 무엇인지와 Python으로 간단하게 함수 구현을 해보도록 한다.

활성화 함수(Activation function)

활성화 함수란 신호의 총합을 받아서 다음 신호로 내보낼지 말지를 결정하는 함수를 이야기 한다. 활성화 함수에는 사실 시그모이드(Sigmoid)와 렐루(Relu)함수 외에도 많은 활성화 함수들이 있다. 그중에서도 가장 기본적인 활성화 함수인 Sigmoid, Relu, Softmax 이 3가지에 대해 알아보겠다.

시그모이드(Sigmoid)

시그모이드 함수는 0에서 1사이의 실수를 출력하는 함수를 이야기한다.

$h(x)= \frac { 1 }{ 1+exp(-x) }$

시그모이드는 자연 상수인 exp을 사용하는데, 덕분에 나중에는 vanishing 현상을 일으키고는 한다.
vanishing현상은 레이어의 깊이가 깊어질수록 신경망이 죽는 현상을 이야기 한다. 시그모이드가 포화되어서 가중치가 죽었다라고도 이야기 할 수 있으며, 조금 더 쉽게 예를 들면 0.9 라는 가중치가 있을 때, 업데이트를 위해 똑같이 0.9 * 0.9 * 0.9 …. 을 100번 반복했다고 했을때를 생각 하면 쉽다. 또한 반대로 0.01이라는 가중치가 있을 때, 100번 업데이트를 한다고 하면 0.01 * 0.01 * 0.01 … 반복하게 되는데 점점 작아지는 것을 알 수있다. 또한 Relu보다는 약 4배정도 느린데, 그 이유는 모든 값을 실수로 0에서 1사이로 변환해서 계산하기 때문이다.

시그모이드 함수는 아래의 코드와 같다.

import numpy as np

def sigmoid(x):
    return 1/(1+np.exp(-x))
    
x = np.array([1.0,2.0])
print(sigmoid(x))

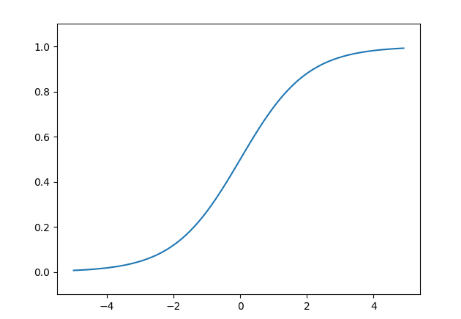
시그모이드 그래프는 아래와 같이 그릴 수 있다.

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5, 5, 0.1)  # -5부터 5 사이에 0.1 간격으로 x에 담아라
y = sigmoid(x)

plt.plot(x,y)
plt.ylim(-0.1, 1.1 ) 
plt.show()

위 코드로 그래프를 출력하면 아래와 같이 출력되는 것을 확인 할수 있다.

sigmoid

Relu (Rectifued Linear Unit)

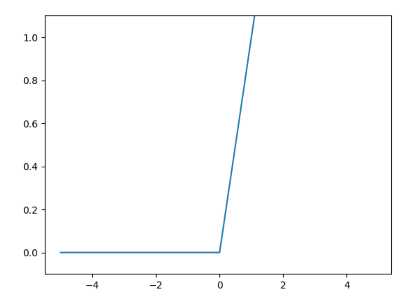
렐루 함수는 입력이 0을 넘으면 그 입력을 그대로 출력하고 0이하면 0을 출력하는 함수이다. 비교적 간단한 수식과 가장 이해하기 쉬운 함수이면서도 현업에서도 가장 많이 사용하는 함수이다.

Relu함수를 Python으로 구현하면 아래와 같다.

def relu(x):
    if x > 0:
        return x
    else:
        return 0

print(relu(-2)) # 0
print(relu(0.3)) # 0.3

그래프는 아래와 같다.

import numpy as np
import matplotlib.pylab as plt

def relu(x):
    return np.maximum(0,x)

x = np.arange(-5, 5, 0.1)  # -5부터 5 사이에 0.1 간격으로 x에 담아라
y = relu(x)

plt.plot(x,y)
plt.ylim(-0.1, 1.1 ) 
plt.show()

relu

소프트맥스(softmax)

소프트맥스(softmax)는 다른 활성화 함수와 다르게 마지막 출력층에서 사용하는 함수이다.
소프트맥스(softmax)함수는 0 ~ 1 사이의 숫자로 출력되는 함수이기는 소프트맥스를 거쳐서 나온 실수의 합은 무조건 1이 되는 함수이다.

[1.2],[0.9],[0.4]의 값이 있다고 할때, 소프트 맥스 함수를 거치고 나온 실수들이 [0.46],[0.34],[0.20]의 실수값이 나왔다. 이 실수들을 전부 다 합치게 되면 1이 된다. 이것을 확률로 나타내면 46%/ 34% /20% 이런식으로 표현할 수 있다. 그래서 주로 분류 문제에서 자주 사용 되곤 하는데 대표적으로 mnist 데이터가 되겠다. 필기체 숫자가 있을 때, 어떠한 이미지가 숫자 1인 확률/ 2인 확률 … 하는 확률 문제에서 풀수 있다.

소프트맥스 함수는 아래와 같다.

def softmaxFunction(x):
    expX = np.exp(x) 
    sumExpX = np.sum(expX) 
    return expX / sumExpX

a = np.array([2.3, -0.9, 3.6])
y4 = softmaxFunction(a)
print(y4, np.sum(y4))

아래와 같이 소프트 맥스 함수를 사용하게 된다면 nan 값을 볼 수 있다.

def softmaxFunction(x):
    expX = np.exp(x) 
    sumExpX = np.sum(expX) 
    return expX / sumExpX

a = np.array([900, 1000, 1000])
y4 = softmaxFunction(a)
print(y4, np.sum(y4))

nan 값을 확인 할수 있다. 소프트 맥스 함수 구현시 문제점이 바로 이것이다.
지수함수를 사용하다보니 계산 결과가 너무 크면 오버플로(너무 큰값을 표현할 수 없는 문제)를 야기하는데, 주로 입력신호 중 최댓값을 이용하면 이 문제를 해결 수 있다.

고쳐진 최종 소프트맥스 함수 코드는 아래와 같다.

def softmaxFunction(x):
    expX = np.exp(x - np.max(x)) 
    sumExpX = np.sum(expX) 
    return expX / sumExpX

a = np.array([900, 1000, 1000])
y4 = softmaxFunction(a)
print(y4, np.sum(y4))