Batch Nomalization 학습 실제 사용할때 주의 할 점

오늘은 Batch Nomalization 학습 실제 사용할때 주의 할 점과 가중치 초기화의 중요성에 대해 같이 보도록 하겠습니다.

가중치 초기화의 중요성

가중치 초기값을 적절하게 설정하면 각 층의 활성화 값의 분포가 적당히 퍼지는 효과가 발생합니다. 그리고 활성화 값이 적절하게 분포하게 되면 학습이 잘되고 정확도가 높아집니다.

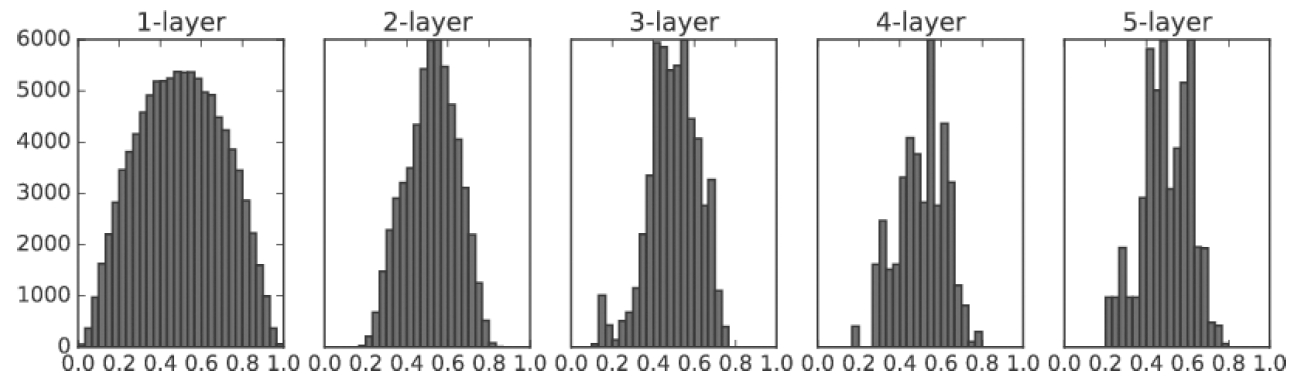
아래의 그림은 학습이 잘 안되는 가중치 분포의 예입니다.

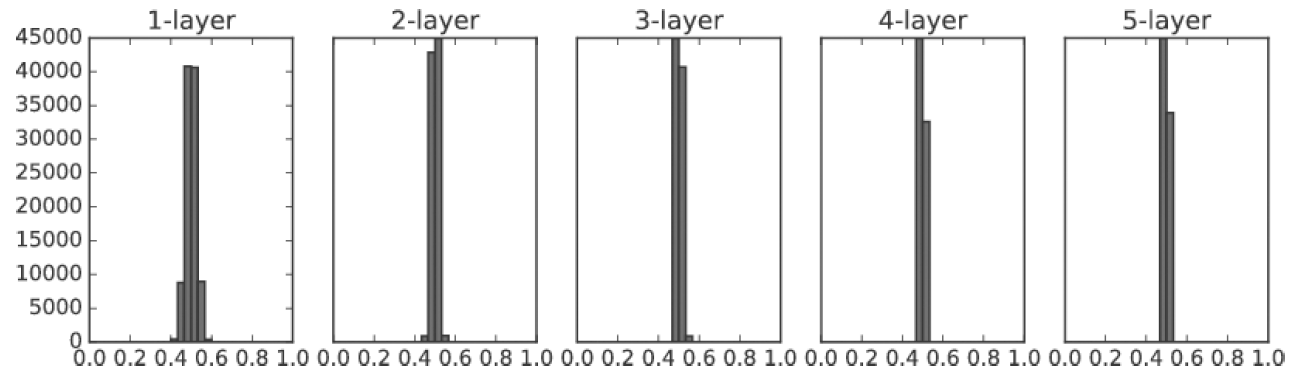
weight1

아래의 그림은 학습이 잘된 경우입니다.

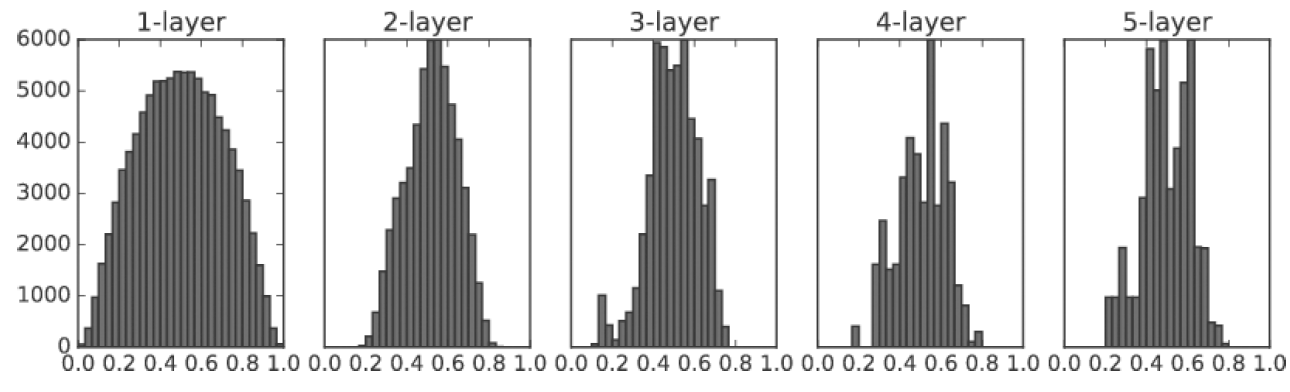
weight2

한 눈에 봐도 고르게 잘 된것을 알 수 있습니다.

가중치 초기값 선정하는 5가지 방법

가중치 초기값을 선정하는 방법에는 대략 5가지 정도가 있습니다.

1. 가중치 초기값을 0으로 선정.

이 방법은 추천하지 않습니다. 왜냐하면 학습이 잘되지 않기 때문이죠.
하지만 이런 방법도 예전에 있는 있었다. 로 넘어가시면 될 것 같습니다.

2. 표준편차가 1인 정규분포를 사용해 초기값 선정.

표준편차가 클수룩 Data가 더 많이 흩어져 있습니다.
ex) 시험문제가 어려우면 아주 잘하는 학생들과 아주 못하는 학생들로 점수가 딱 나눠진다.

1 * np.random.randm(10,100)

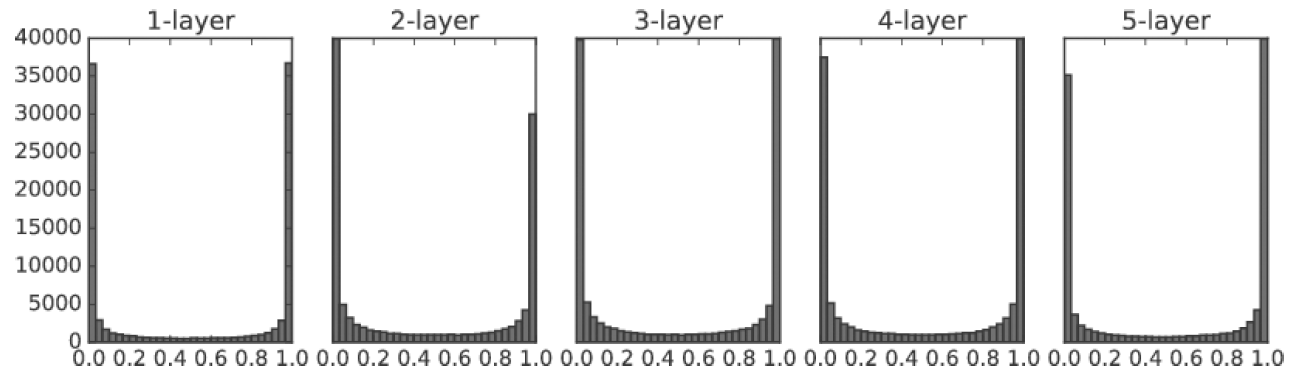
weight3

3. 표준편차가 0.01인 정규분포를 사용해 초기값 선정.

표준편차가 작을수록 Data가 평균에 가깝게 분포합니다. ex) 시험문제가 쉬우면 학생들 점수가 평균에 가깝다.

0.01 * np.random.randm(10,100)

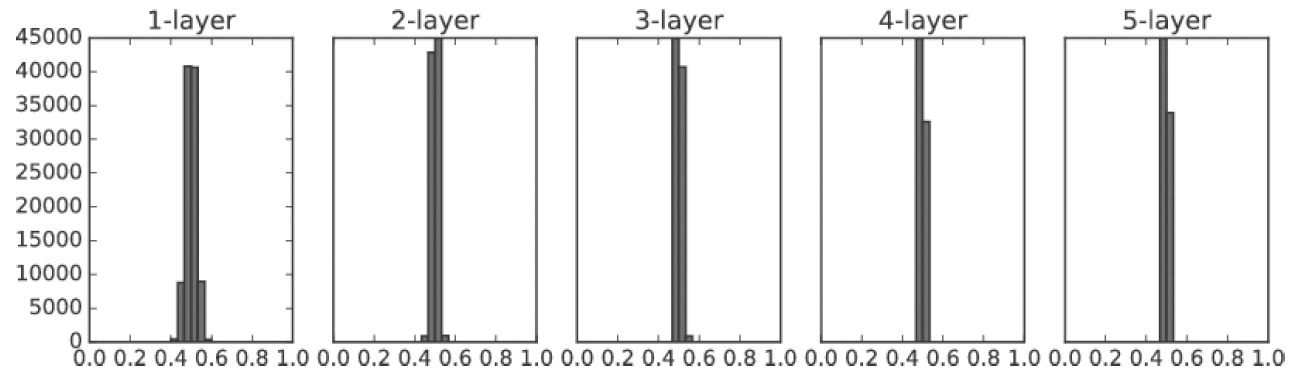
weight4

4.Xavier 초기값 선정.

표준편차가 √(1/n)인 (n은 앞층의 노드 수) 정규분포로 초기화하는 방법이 있으며 sigmoid 함수와 짝궁이며 같이 사용됩니다.

weight5

5.He 초기값 선정.

표준편차 √(2/n)인 정규분포로 초기화하는 방법이 있습니다. He는 Relu함수와 짝궁으로 같이 사용됩니다.

배치 정규화

앞에서 가중치 초기값을 적절하게 설정하면 각 층의 활성화 값이 적절하게 분포하여 학습이 잘되고 정확도가 높아지는 것 또한 알 수 있었습니다.

그러나 가중치 초기화를 하더라도 가중치 값이 불규칙하게 분포할 가능성이 있습니다. 여기서 배치 정규화의 개념을 툭 튀어나오게 됩니다. 배치 정규화는 바로 각 층에서 활성화 값이 적당하게 분포 되도록 강제로 조정하게 합니다.

여기서 가장 중요한 사실은 Training data 전체에 대해 mean과 variance를 구하는 것이 아니라, mini batch 단위로 접근하여 계산합니다. 현재 택한 mini batch 안에서만 mean과 variance를 구해서 이 값을 이용해서 mormalize 합니다.

즉, 학습 시 미니배치를 단위로 정구화를 하며, 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화 합니다.

${ \mu }_{ B }\quad \leftarrow \frac { 1 }{ m } \sum _{ i=1 }^{ m }{ x_{ i } }$

평균

${ \sigma }^{ 2 }_{ B }\quad \leftarrow \frac { 1 }{ m } \sum _{ i=1 }^{ m }{ (x_{ i }- } { \mu }_{ B })^{ { 2 } }$

분산

${ \hat { x } }_{ i }\leftarrow \frac { { x }_{ i }-\mu _{ { B } } }{ \sqrt { { \sigma }_{ B }^{ 2 } } +E }$

실제 값 - 평균 , 표준편차 + E

왜 층마다 배치 정규화 작업을 해야 할까요? 그 이유는 신경망은 파라미터(매개변수)가 많기 때문에 학습이 어렵습니다. 특히나 딥러닝 같은 경우는 레이어가 많은데 이 뜻은 가중치가 층마다 다르다 라고 해석 할 수 있습니다. 더욱이 층을 통과할수록 각기 다른 가중치가 쌓이며 가중치의 작은 변화가 가중 되어서 쌓이면 레이어가 많아 질수록 출력되는 값의 변화가 크기 때문입니다.

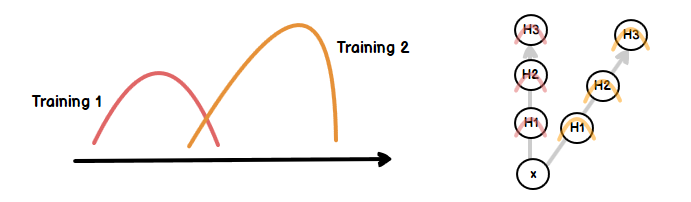
batch1

즉, 가중치 때문에 입력값에 대한 완전히 다른 출력값이 나옴을 알 수 있습니다.

이러한 이유로 배치 정규화가 등장했으며, 배치 정규화는 입력값이 활성화 함수를 통과하기 전에 가중의 변화를 줄이는 것이 목표입니다. 가중의 합이 배치 정규화에 들어오게 되면 기존 값의 스케일을 정규분포로 조정하게 되며 선형이 아닌 비선형 사이로 분포를 유지하여 데이터의 폭(scale), 분포(shift)의 위치를 조절하기 위해 감마(분산)과 베타(평균)을 적용하여 이를 학습하면서 층을 거치게 됩니다.

Batch Normalization 을 사용할 때의 주의할 점.

배치 정규화를 하는 이유는 학습을 하기 위해서 라고 했습니다. 훈련 데이터를 통해서 이미 감마(분산)값과 베타(평균)값이 이미 최적에 맞춰진 상황입니다. 이 모델을 이용하여 테스트를 수행하려고 할 경우 훈련 데이터의 평군, 표준편차 값과 테스트 데이터의 평균, 표준편차 데이터가 다르기 때문에 제대로 테스트 되지 않을 수 있습니다.

즉, 훈련 데이터의 최적의 감마, 베타 값을 가지고 테스트를 하면 값이 제대로 나올 수 있기 때문에 테스트 데이터로 모델을 돌릴 때에는 배치 정규화를 사용하면 안됩니다.

학습 단계에서는 데이터 단위가 배치 단위로 들어오기 때문에 배치의 평균, 분산을 구하는 것이 가능하지만 테스트 단계에서는 배치 단위로 평균/분산을 구하기 어렵습니다. 이를 해결하기 위해서는 두가지 방법이 있습니다.

1. 학습 단계에서 배치 단위의 평균/ 분산을 저장. (이동평균)
2. 테스트시에는 구해진 이동평균을 사용하여 정규화.

Training Data로 학습을 시킬 때는 현재 보고 있는 mini batch에서 평균과 표준 편차를 구하지만, Test Data를 사용하여 Inference를 할 때는 다소 다른 방법을 사용합니다. mini batch의 값들을 이용하는 대신 지금까지 본 전체 데이터를 다 사용한다는 느낌으로, Training할 때 현재까지 본 Input들의 이동평균 및 비편향추정량의 이동평균을 계산하여 저장해놓은 뒤 이 값으로 normalize를 합니다. 마지막에 감마와 베타를 이용하여 scale/shift 해주는 것은 동일합니다.