강화학습에서의 자주 거론되는 min/max 알고리즘에 대해 자세히 알아보겠습니다.

min/max 알고리즘

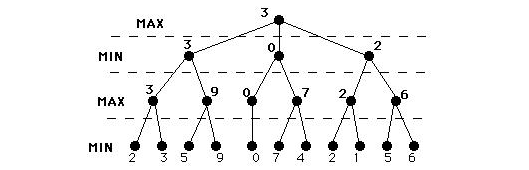
min/max 알고리즘에서 max는 나를 뜻하는 것이고 min는 적을 이야기 합니다. 탐색전에 트리는 맨 아래 단계만 의미있는 수를 가지며, 탐색이 진행되면서 하위에서 상위로 값을 찾아 올라가게 되는데 이때 상위 노드에서 선택되는 값은 현 단계가 max이면 아래에서 최대값을, 현 단계에서 min이면 아래에서 최소값을 선택하게 됩니다.

즉, 나(컴퓨터)는 가장 큰 수를 취해야 하며, 상대(사람)은 가장 작은 수를 취해야 합니다.
양수(+ ∞)는 내가 이긴 것(컴퓨터)이고, 음수(- ∞)는 내가 진 것(사람)을 이야기합니다.

강화학습으로 Tic Tac Toe을 학습한다고 했을 때, 평가 함수 e와 상태 함수 p가 있다고 가정하고 이야기 하면 아래와 같습니다.

1. 상태 함수 p가 양쪽 모두에게 이기는 상황이 아니라면
   e(p) = (Max에게 가능한 행, 열, 대각선 수) - (Min에게 가능한 행, 열, 대각선 수)

2. 상태 함수 p가 Max에게 이기는 상황 (컴퓨터가 이기는 상황)
   e(p) = + ∞

3. 상태 함수 p가 Min에게 이기는 상황(사람이 이기는 상황)
   e(p)= - ∞

정리하자면, 숫자는 평가 함수 e에 의해서 결정이 되는데,

• Max는 숫자가 큰 값을 선택해야 자신이 이길 경우의 수가 더 많은 경우로 나아갈 수 있습니다.
• Min은 숫자가 적은 값을 선택해야 자신이 이길 수 있는 경우의 수가 많은 값으로 나아갈 수 있습니다.

Tic Tac Toe으로 결정 과정을 보면 아래 그림과 같습니다.

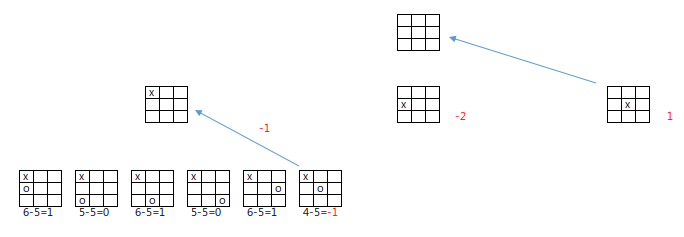
상대방 수는 가장 작은 수를 올리고 내 수는 가장 큰 수를 올립니다.

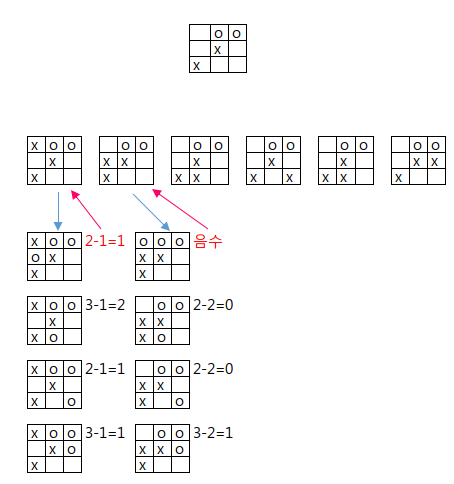
상대가 두는 턴(사람)↑

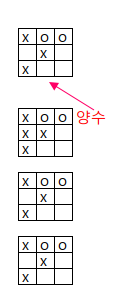
내가 두는 턴(컴퓨터)↑

그러나 오목이나 바둑 같은 경우는 트리가 굉장히 크기 때문에 이 문제를 해결하기 위해 나온 알고리즘이 알파베타프루니입니다. 이 부분에서는 다음에 다시 다루겠습니다.