강화 학습에서 빠질 수 없는 몬테카를로 알고리즘에 대해 자세히 알아보겠습니다.

몬테카를로 알고리즘

몬테카를로 알고리즘의 원리는 멘땅의 해딩을 여러번 반복하다 보니, 답을 알게 되었다 입니다. 확률의 종류는 3가지로 볼 수 있습니다.

1. 수학적 확률: 경험을 하지 않고도 미리 알 수 있는 확률로 동전을 던질 때, 앞면이 나올 확률은 굳이 경험하지 않아도 수학적으로 구할 수 있는 확률

2. 통계적 확률: 똑같은 조건에서 아주 오랫동안 과거의 경험을 바탕으로 확률을 구하는 방법.
예를 들어 비가 올 확률과 같이 과거의 데이터를 바탕으로 얻는 경험적 확률입니다.

3. 기하학적 확률: 1777년 프랑스 수학적인 조르주주이르클레이드뷔퐁이 제시한 ‘바늘 문제’에서 유명해졌습니다. 바늘 문제란 바늘이 여러개의 평행선을 그은 평면 위에 던질 때, 바늘이 평행선 가운데 하나와 만날 확률이 얼마인지를 따지는 문제인데, 이 문제로 원주율 값을 알아냈다.

몬테카를로 트리 탐색

“수를 두기 전에 미리 수를 다 넣어보고 가장 좋은 결과 값으로 수를 둔다” 또는 “랜덤을 발생시켜서 해답을 찾아가는 과정”이라고 볼 수 있습니다.

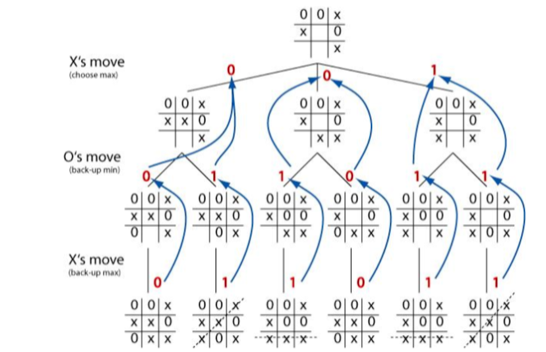
한수를 평가하기 위해서 그것에서 비롯되는 모든 가능성을 탐색하는게 아니라 무작위로 선택한 샘플만을 검토합니다. 샘플 크기를 늘리고 시물레이션 횟수를 증가시키면 모든 가능성을 검토한 것과 같은 결과가 나옵니다.

몬테카를로 알고리즘이 필요한 이유

많은 요소들이 작용하는 불확실한 상황에서 의사결정을 하기 위해서입니다. 랜덤 값을 발생시켜 시물레이션을 함으로써 직접 계산하기 어려운 복잡한 수치들을 구할 필요가 있을 때 유용합니다. 실제 세상에서 발생되는 거의 모든 일들은 확률로 설명될 수 있습니다.

이러한 확률적 현상들을 수학적으로 풀고 싶은데, 그것이 수학적으로 정밀하게 풀어낼 수 없을 때 랜덤 값을 발생시켜 시물레이션함으로서 정답에 근접한 해를 구할 수 있습니다.