고유값과 고유벡터에 대해서 많이 들어봤을 것이다. 그만큼 무척 중요하다고 모두들 이야기한다. 이번에 새롭게 공부하기 시작하면서 고유값과 고유벡터가 무엇인지, 왜 중요한지에 대해 정리해보려고 한다.

고유값, 고유벡터란?

대부분 벡터 x에 어떤 행렬 A를 곱하게 되면 벡터의 크기와 방향이 바뀌게 된다. 그러나 정방행렬에 정방행렬의 고유벡터를 곱하면 고유벡터의 방향이 바뀌지 않는다 더 간단히 말하면 벡터x가 행렬 A의 고유벡터라면 바뀌지 않는다.

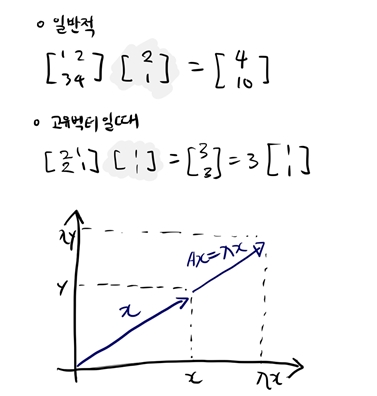
선형 변환은 어떤 벡터 공간에 속하는 벡터를 다른 벡터로 매핑하는 함수인데, 이 변환을 수행할 때 변환된 벡터가 원래 벡터와 동일한 방향을 유지하거나 반대 방향을 가르키면서 오직 크기만 변하는 경우가 있다. 이러한 특별한 벡터가 고유 벡터이며, 이들의 크기 변화율을 나타내는 값이 고유 벡터이다.

고유값과 고유벡터의 수학적 정의

선형 변환을 나타내는 $A$ 라는 행렬이 있을 때 고유 벡터 $v$와 이에 대응하는 고유값 $λ$에 대한 관계는 아래와 같이 표현한다.

• $A$는 선형 변환을 나타내는 행렬
• $v$는 고유벡터로 $A$에 의해 변환된 후에도 방향이 변하지 않는 벡터
• $λ$는 고유값으로 선형 변환에 의해 $v$가 스케일 되는 비율

고유값 문제를 푼다는 것은 주어진 선형 변환 $A$에 대해 위의 방정식을 만족하는 $λ$와 $v$를 찾는 것이며, 이는 아래와 같은 의미를 갖는다.

• 고유벡터$v$의 방향 : 이 벡터들은 $A$에 의해 변환될 때, 그 방향이 유지된다. 즉, 고유벡터는 선형 변환을 거친 후에도 원점으로부터 멀어지거나 가까워지는 방향으로만 이동하며, 이 방향은 변환 전후로 일정하다.

• 고유값$λ$이 나타내는 의미: 고유값은 고유벡터가 선형 변환을 거치면서 스케일링되는 정도를 나타낸다. 고유값이 1보다 크면 벡터는 원점으로부터 멀어지고(확장), 1보다 작으면 원점으로 가까워집니다(수축). 고유값이 음수일 경우, 벡터는 방향이 반대로 변하면서 스케일링된다.

왜 중요한가 ?

고유값과 고유벡터는 어떤 행렬의 가장 굉장히 중요한 정보를 담고 있다. 임의의 벡터를 어느 방향으로 변화시켰는지, 변환 과정에서 변화 없이 유지는 되는 부분은 어느 부분인지를 말한다. 어떠한 물체나 영상 등 이들은 무수히 많은 벡터들의 뭉치라고 이야기 할 수 있는데, 고유값과 고유벡터로 인해 영상이나 물체가 어떤식으로 변화되고 중심축은 어디인지에 관한 중요한 정보들을 파악할 수 있다. 응용분야에는 PCA, EigenFace 가 있다.