예전 포스팅에 미분이 필요한 이유에 대해서 정말 잠깐 이야기 했었는데, 블로그 정리하면서 보니 설명이 부족한거 같아 좀 더 정리할 겸 이렇게 글을 쓰게 되었다.

다항식

머신러닝에서 비선형 함수를 어떻게 추측해낼까? 우선 비선형 함수를 가장 간단하게 표현하면 아래와 같이 다항식으로 표현할 수 있다.

$h_{\theta }\left ( x \right )= \theta _{0} + \theta _{1}x + \theta _{2}x^{2} + \theta _{3}x^{3} + \theta _{4}x^{4} + \theta _{5}x^{5}$

0차나 1차식을 제외한 모든 다항식은 전부 비선형으로 표현 할 수 있다. 이런 다항식들로 다항식 형태가 아닌 함수들도 근사치를 표현할 수 있다. 그리고 이때, 근사치의 n차 다항식을 찾아내는 작업을 미분방정식에서 Taylor expansion으로 배운다.

Taylor expansion

그래서 오늘은 이 Taylor expansion에 대해 이야기 해볼까 한다. Taylor expansion를 이용한 비선형을 다항식화 한다고 하면 아래 식과 같이 근사 다항 함수로 표현하면 아래와 같이 표현 할 수 있다.

$f(x+h) = f(x)+ {f}'(x)h + {f}''(x)\frac{h^{2}}{2!}+{f}'''(x)\frac{h^{3}}{3!} + ... $

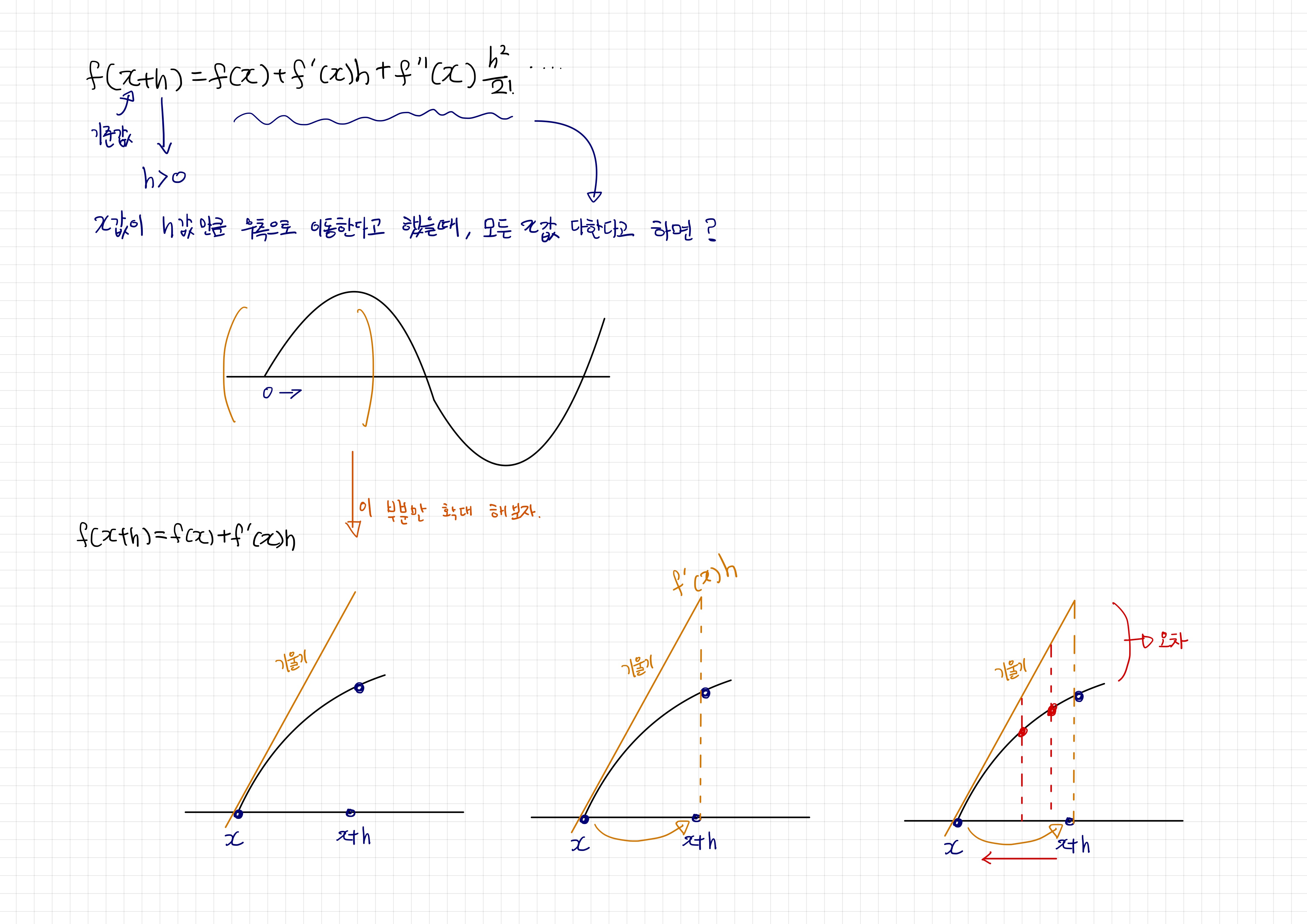
식을 정말 간단하게 설명하자면 x가 h값만큼 이동 했을때의 기울기와 값을 구하려고 한다.
그래서 f(x+h) 즉, x가 h만큼 이동 했을 때의 값 {f}’(x)h를 알 수 있게 된다.

오차항

그러나 위 그림의 오른쪽 그림과 같이 오차가 발생할 수 밖에 없다. 이론적으로 n이 무한대가 되면 오차는 0의 완벽한 근사치 다항식을 만들 수 있지만, 그렇게 되면 계산이 끝도 없기 때문에 보통은 n=2 , n=3정도로 타협하고 나머지 항목을 오차항이라고 부른다.

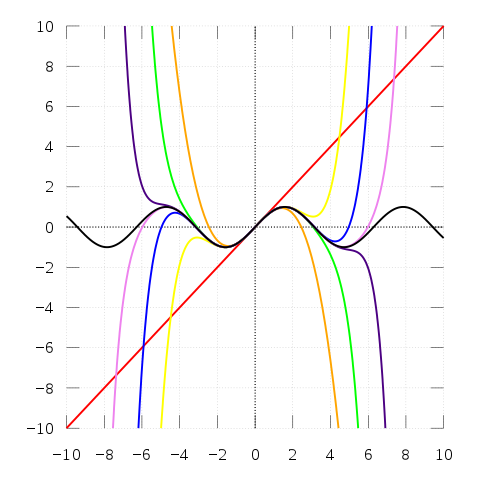
위 그래프처럼 다차항이 커짐에 따라 실제 데이터와의 fitting이 점점 증가한 모습을 볼 수 있으며, 만약 실제 데이터에 적용한다면 아래의 그림과 같다.

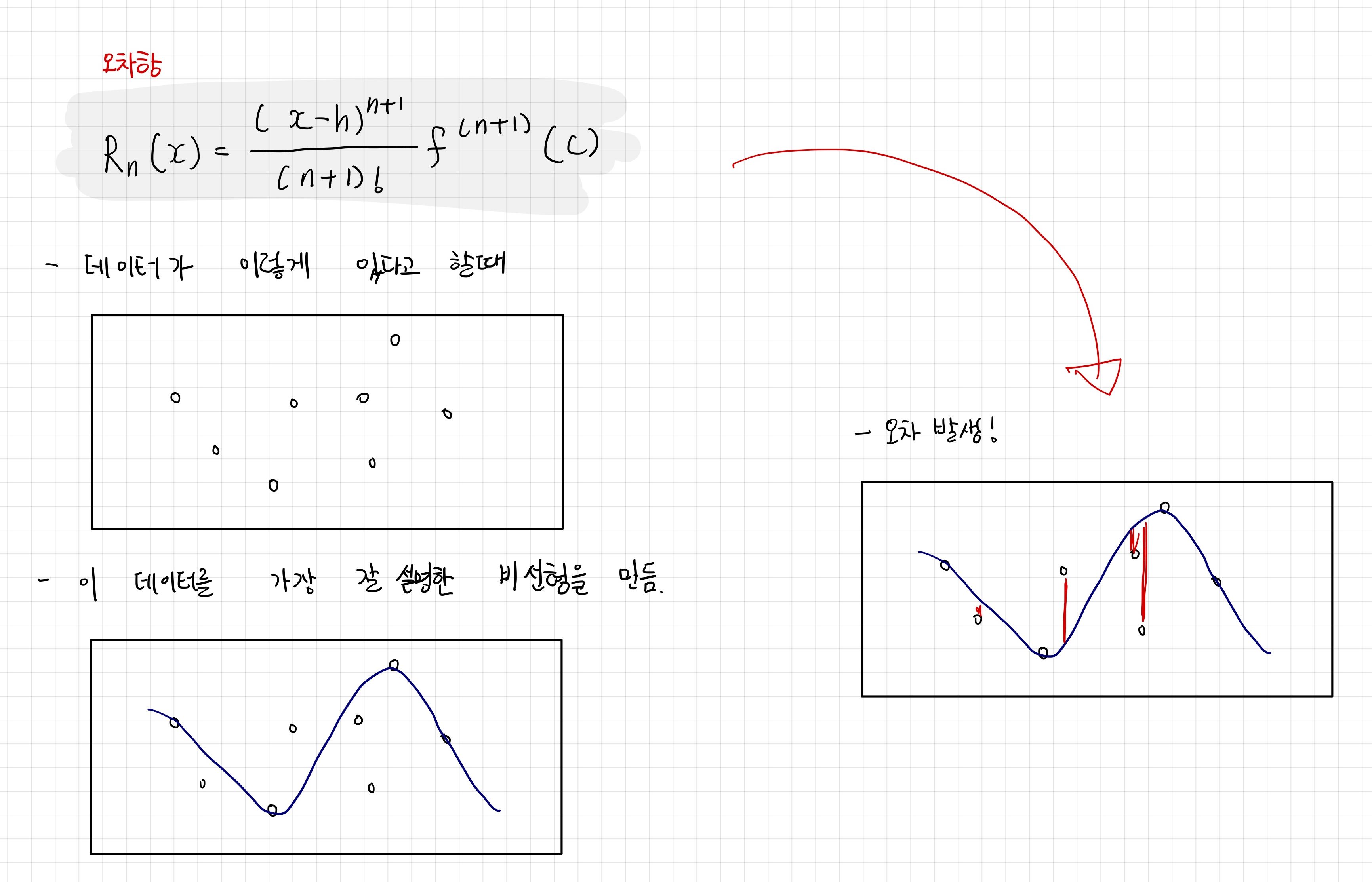
이렇게 미적분은 기본적으로 많이 사용되니 왜 사용하는지 잘 알아두는 것이 좋다.