오랜만에 확률 모형과 확률 변수, 그리고 PDF, CDF 등에 대해 글을 쓰려고 했는데 집중력이 떨어져서 그런지 머릿속으로 그림이 흐려져서 다시 한번 그려볼겸 글을 쓴다.
이번 포스팅의 내용을 요약하면 아래의 그림과 같다.
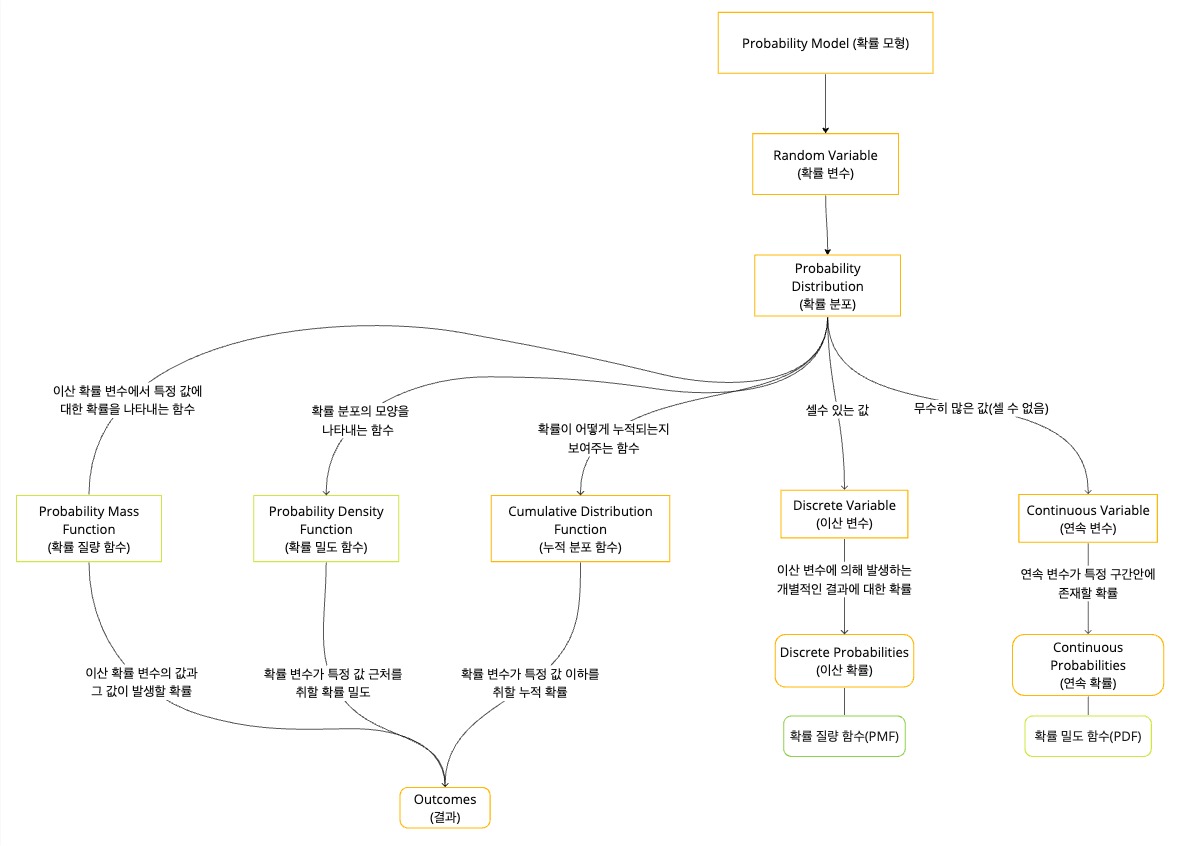
요즘 다이어그램 그리는게 재미있어서 그려봤는데, 한번 그려보니 먼가 이해하기 더 편해진 기분이다.
확률 모형, 확률 변수, 확률 분포 … 사실 너무 헷갈린다.. (나는 적어도 그렇다..ㅠ)
그래서 확률 모형, 확률 변수, 확률 분포를 어떻게하면 쉽고 헷갈리지 않을 수 있을까를 곰곰히 생각했고 나는 아래와 같이 설명할려고 한다.
-
확률 모형(Random Variable)
동전을 던졌을 때 앞면(Head)이 나올지 뒷면(Tail)이 나올지를 설명하는 전체적인 “규칙”이다.
-
확률 변수(Random Variable)
동전 던지기의 결과를 나타내는 “변수”로 앞면을 H, 뒷면을 T로 나타내기로 했다.
-
확률 분포(Probability Distribution)
동전이 앞면이 될 확률(50%)와 뒷면이 될 확률(50%)를 나타내기 때문에 동전 던지기의 결과의 확률을 설명할 수 있다.
-
이산 확률 함수(Discrete Probability Function)
이산 확률은 각각의 별개의 결과에 대한 확률을 제공하는데, 동전은 앞면, 뒤면 두가지의 결과가 있고, 확률 질량 함수(PMF)를 사용하여 각 결과에 확률을 할당한다면, 앞면이 나올 확률은 50%, 뒷면이 나올 확률은 50%로 나타낼 수 있다. -
결과
실제 동전이 던저서 나오는 결과이며, 앞면 또는 뒷면이 나올 수 있으며 이는 확률 모형이 설명하려는 사건의 결과다.
이제 더 자세하게 알아보자.
확률 모형
확률 모형은 랜덤한 사건의 결과를 수학적으로 모델링한 것을 말한다. 불확실성을 가진 사건이나 행동을 이해하고 예측하기 위해 사용한다. 확률 모형은 확률 변수, 확률 분포, 확률 과정 등에 포함할 수 있다.
확률 변수(Random Variable)
확률 변수에서 우선 변수는 무엇일까?
코딩에서 변수는 어떤 값을 나타내는 기호로 쓰지만, 수학적 표현에서의 변수는 특정한 범위 내의 값을 취할 수 있는 불확정적인 요소를 말한다.
확률 변수에서의 변수는 특정 확률 실험 또는 랜덤으로 나타나는 여러 가지 가능한 값 중 하나를 취하는 것을 말하며, 확률 변수는 이러한 랜덤한 사건의 결과들에 대한 분포를 통해 그 값의 확률을 수치적으로 표현한 것이다.
위 그림에서 한번 봤겟지만, 확률 변수에는 여러 유형의 확률 변수가 있다. 대표적으로 이산 확률과 연속 확률 변수가 있으며 이외에도 다변량 확률 변수, 정수형 확률 변수, 범주형 확률 변수 등이 있다.
-
이산 확률 변수 (Discrete Random Variable) : 셀 수 있는 값(0,1,2..)을 말한다.
-
연속 확률 변수 (Continuous Random Variable) : 연속적인 값을 가지며, 보통 실수의 범위로 표현한다.
연속 확률 변수는 예시에 적혀 있듯 값을 구하려면 확률 밀도 함수(PDF)와 같은 모델링을 통해야지만 값을 알 수 있다. 왜 그럴까?
연속 확률 변수는 특정한 값을 가지는 대신 값의 범위를 통해 확률을 표현한다. 왜냐하면, 무한히 많은 가능한 값들을 가질 수 있고, 미세한 차이로 끊임없이 변화할 수 있기 때문이다. 예를 들어 어떤 지점에서의 온도나 사람의 키와 같은 연속적인 측정값은 정확히 같은 값을 두 번 측정하기 어렵기 때문이다. 이러한 이유로 연속 확률 변수의 특정 값에 대한 확률을 직접으로 계산하는 것이 의미가 없기 때문에 확률을 구간을 통해 정의하며, 확률 밀도 함수는 이러한 연속 확률 변수의 성질을 모델링하는 데 적합하다.
확률 분포
아까 처음에 예시로 들었던 “동전 던지기” 예시를 보면 확률 분포와 이산 확률 함수의 설명과 상당히 유사하다. 이미 PMF로 각 결과에 확률을 할당했는데 확률 분포가 의미가 있을까?
확률 분포는 확률 변수의 모든 가능한 결과와 그 결과들이 발생할 확률을 말하는 함수이다. 확률 분포는 아래와 같은 중요한 역할을 한다.
- 확률 변수의 전체적인 행동을 이해할 수 있다.
- 확률 변수의 성질을 파악해, 확률 변수가 이산인지, 연속인지, 분포의 형태가 어떠한지(균등, 정규, 이항)를 알 수 있다.
- 확률 분포는 사건에 대한 예측을 할 때 기초가 되는 정보를 제공하는데, 예를 들어 확률 분포를 바탕으로 평균, 분산, 표준 편차을 계산한다.
확률 질량 함수 (probability mass function, PMF)
이산 확률 변수의 각 가능한 값에 대한 확률을 나타내는 함수이다. ‘이산’ 이라는 말은 확률 변수가 취할 수 있는 값들이 개별적이고, 분리된 값을 의미한다.(예를 들어 0,1,2,…) PMF는 이산 확률 변수가 특정 값에 대해 가지는 확률을 말한다.
PMF는 함수 $f(x)$ 를 통해 정의되며, 이산 확률 변수 $X$가 특정 값 $x$를 가질 확률을 $P(X=x)$로 나타낼 수 있다. 모든 확률은 0과 1사이의 값을 가지며, $0≤f(x) ≤ 1$ 이다.
이산 확률 변수가 가질 수 있는 모든 값에 대한 PMF의 합은 1이고, $∑_{allx} f(x)=1$ 로 표현할 수 있다.
확률 밀도 함수(probability density function, PDF)
연속 확률 변수가 특정 구간 내에서 값을 취할 확률의 밀도를 나타내는 함수이다. 연속 확률 변수는 셀 수 없이 많은 값들을 가질 수 있기 때문에 PDF는 특정 값이 아닌 값의 범위에 대한 확률을 설명한다.
PDF는 함수 $f(x)$를 통해 정의되며, 연속 확률 변수 $X$가 특정 값에 있을 확률의 밀도를 나타낸다. 연속 확률 변수가 특정 값 $x$를 정확히 가질 확률은 0이지만, PDF는 특정 구간에서 확률 변수의 값이 존재할 확률을 구하기 위해 해당 구간에 대해 적분을 사용한다. 예를 들어, $X$가 구간 $[a,b]$안에 있을 확률은 $\int_{a}^{b} f(x) dx$로 계산한다. PDF는 확률이 아닌 밀도이기 때문에 1보다 클 수도 있지만, 적분을 통해 확률을 구하기 때문에 항상 0과 1사이의 값을 갖는다. 따라서 모든 가능한 값에 대한 확률의 총합은 $\int_{−∞}^{∞} f(x) dx = 1$ 로 표현한다.
누적 분포 함수 (cumulative distribution function, CDF)
확률 변수가 특정 값 이하의 값을 취할 확률을 나타내는 함수이다. 이산 확률 변수와 연속 확률 변수 모두에 적용할 수 있고, 확률 분포의 전체적인 행동을 이해하는데 매우 유용하다.
CDF는 함수 $F(x)$를 통해 정의하며, 확률 변수 $X$가 특정 값 $x$보다 작거나 같을 확률을 나타내고 $F(x) = P(X ≤ x)$로 표현한다. 값은 항상 0과 1사이를 가지며, $X$가 모든 가능한 값보다 작을 때 CDF는 0에 수렴하고, $X$가 모든 가능한 값보다 클 때 CDF는 1에 수렴한다.
CDF는 항상 오른쪽으로 비스듬히 증가하는 형태를 가지기 때문에 감소하지 않는 함수이다. CDF는 확률 변수의 중앙값, 사분위수 등을 결정하는데 사용되거나, 확률 변수가 특정 범위에 속할 확률을 구할 때 CDF의 차이를 사용한다.
참고로 이외에도 여러 확률 분포와 여러 확률 함수가 있기 때문에 간단하게 그려보자면 아래처럼 그릴 수 있다.

