회귀는 하나의 변수가 나머지 다른 변수들과의 선형적 관계를 갖는가의 여부를 분석하는 하나의 방법이디. 즉 하나의 종속변수와 독립변수 사이의 관계를 명시하는 것을 우리는 회귀라고 한다. 오늘은 회귀가 무엇인지와 구하는 방법에 대해 알아보겠다.

회귀

독립변수와 종속변수는 아래와 같다.

• 독립 변수: 종속 변수의 영향을 주는 변수(평수, 학군)
• 종속 변수: 서로 관계를 가지고 있는 변수들 중에서 다른 변수의 영향을 받는 변수 (집값)

회귀식은 $y = ax + b$ 이며, 정말 간단하다. 회귀식을 이용하여 간단하게 예제 문제를 풀어보겠다.

1986년 1월 28일 미국의 스페이서 셔틀 챌린저호의 승무원 7명이 사망했다. 우주 왕복선이 발사 도중에 폭파해서 사망을 했기 때문이다. 폭파에 대한 원인 분석을 했는데 그 원인이 발사 온도에 대한 o형 링의 파손 때문이라고 한다. 그렇다면 식을 대입해 풀어본다면 아래와 같다.

여기서 a와 b를 구해야는데, 최적의 a(기울기)와 b(절편)을 결정하기 위해 정규 최소 제곱으로 알려진 추정 기법을 사용할 수 있다. 실제 값와 예측값 사이의 수직 직선인 오차(잔차)를 제곱해서 구한 총합을 알아야 한다.

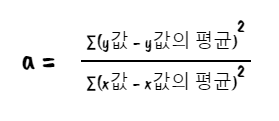사실 식을 깔끔하게 정리하면 아래와 같다.

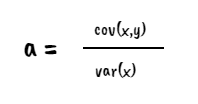
결국 기울기와 절편을 R을 이용해서 구하면 아래와 같다.

a <- cov(challenger$temperature, challenger$distress_ct)/var(challenger$temperature)
b <- mean(challenger$distress_ct)-(a*mean(challenger$temperature))

# a (기울기) = -0.057
# b (절편) = 4.3

만약 온도가 31도고 a가 -0.057이고 b가 4.3임을 알아냈다면 식은 $y = -0.057*31+4.3$이 된다. 약 3개의 링이 파손 되었을거라고 추정할 수 있다.