k-means는 우선 비지도 학습에 속한다. 비지도 학습은 대체로 라벨이 없기 때문에 입력 데이터의 특징을 가지고 자동으로 분류한다. k-means는 그중에서 간단하고 자주 쓰이는 편에 속한다.

k-means

위에서도 말했듯, 요약하면 k-means는 각 문서들 속에 들어있는 데이터 분석을 통해 유사하거나 관계가 높은 항목들끼리 집합을 만들고 싶을 때, 사용하는 알고리즘이다.

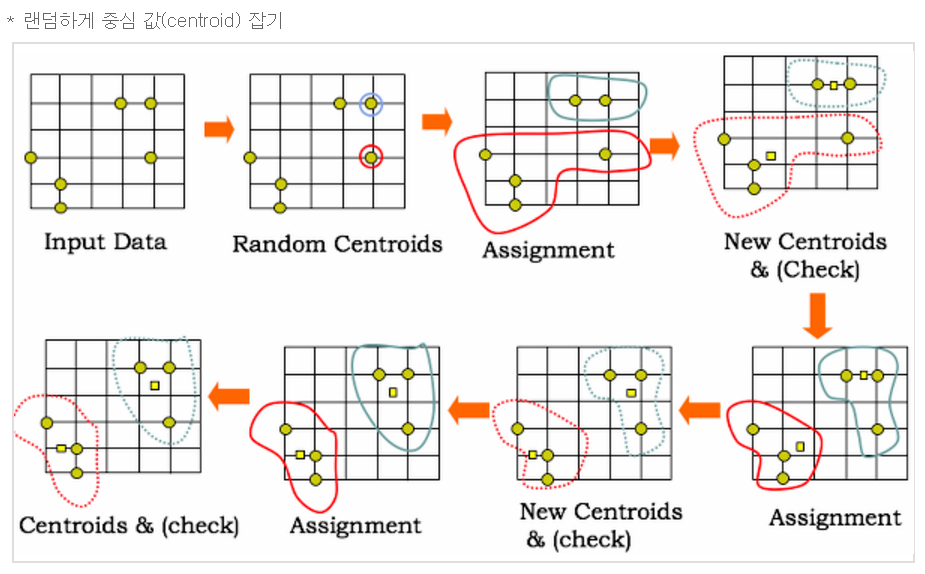
그림을 설명해보자면 아래와 같다.

1. 처음에 중심값을 선택. (랜덤하게 중심값을 선택)
2. 클러스터 할당: k개 (그림 속에서는 2개)의 중심값과 각 개별 거리를 측정한다.
3. 가장 가까운 클러스터에 해당 데이터를 분류한다.
4. 새 중심값 선택 : 클러스터마다 새로운 중심값을 계산한다.
5. 범위 확인 : 선택된 중심값이 변화가 어느정도 없다면 멈춘다. -> 만약 있다면 (1)번부터 반복

k-means 단점

k-means의 단점으로는 이상치(노이즈)에 민감하다는 점이 있다.

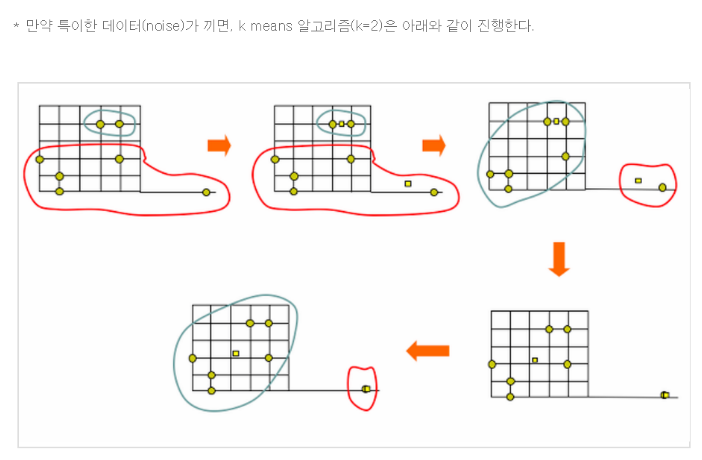
노이즈 데이터를 잘 처리해주지 않으면 이상치 값과 그렇지 않은 값으로 뷴류한다. 정리하면, k-means의 한계점을 뽑자면 아래와 같다.

1. k값 입력 파라미터를 직접 지정해야한다.
2. 이상치에 민감하다.

k-means 예제

기본 데이터 셋을 간단하게 만든다.

c <- c(3,4,1,5,7,9,5,4,6,8,4,5,9,8,7,8,6,7,2,1)
row <- c("A","B","C","D","E","F","G","H","I","J")
col <- c("X","Y")
data <- matrix( c, nrow= 10, ncol=2, byrow=TRUE, dimnames=list(row,col))

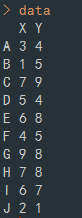
위에서 만든 데이터 셋을 plot 그래프로 그려서 확인하면 아래와 같다.

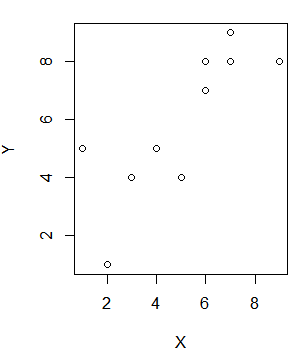
k-mean 패키지 설치 후, 분류하면 아래와 같다.

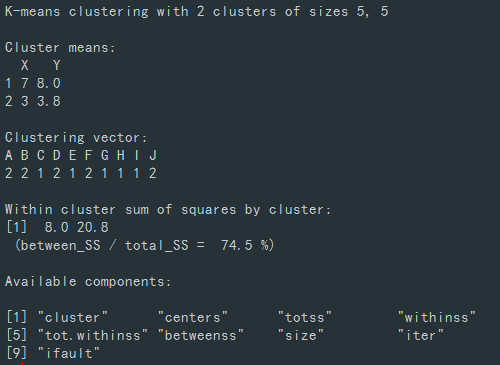
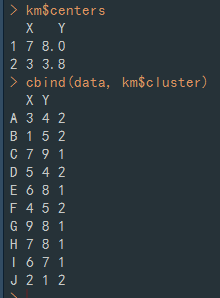
원래 데이터와 겹쳐서 함께 시각화하면 아래와 같다.

plot(round(km$centers), col=km$centers, pch=22, bg=km$centers, xlim=range(0:10), ylim=range(0:10))
par(new=T)
plot(data, col=km$cluster+1, xlim=range(0:10), ylim=range(0:10))

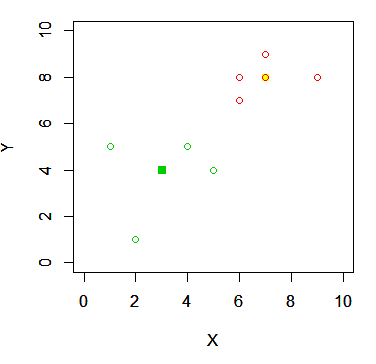
그렇게 어렵지 않게 데이터를 군집화 시킬 수 있기 때문에 간단하게 많이들 돌려보는 편이다. 또한 간단한거 치고는 유용하기 때문에 데이터 분석할때 사용하기 용이하다.