정규분포는 많은 경영, 경제, 사회현상, 자연 현상들이 정규분포의 형태를 띄고 있다. 예를 들면 한국 성인 남자의 평균 키가 173cm라고 하면 키가 173cm에서 크게 벗어나지 않는 사람들이 많고, 상대적으로 이 수치에서 벗어난 150cm, 190cm인 사람들은 별로 없다는 의미이다.

정규분포

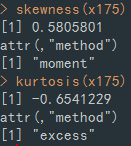
정규분포는 평균에서 멀어질수록 데이터 분포가 감소하여 종모양의 형태를 띈다. 그리고 정규분포 그래프를 3등분하면, 평균 근처의 비율이 68%정도 된다.

## -3 ~3까지의 데이터를 200개 만든다.
x<-seq(-3, 3, length=200)
plot(x, dnorm(x, mean=0, sd=1), type='l', main="정규분포 그래프")

dnorm은 y축이며, mean 평균값, sd는 표준편차이다. type = ‘l’은 직선을 뜻한다.

정규분포 그래프를 보면 데이터가 오른쪽으로 비대칭인지, 왼쪽으로 비대칭인지를 확인할 수 있다.

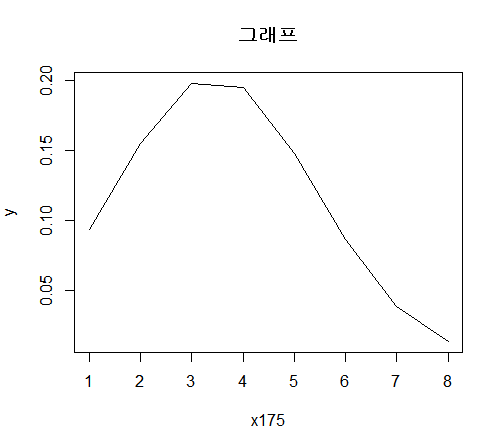
여기서 좌우의 기울어짐의 정도를 뜻하는 용어는 왜도(skewness)라고 하며 (x>0이면, 오른쪽으로 꼬리가 길며, x<0이면 왼쪽으로 꼬리가 길다.) 위아래 뾰족한 정도는 첨도(kurtosis)(3에 가까울수록 정규분포, 3보다 작을수록 완만하다)라고 한다.

아래의 데이터를 넣고 어느쪽으로 편향되어 있는지 정규분포를 그려서 확인해볼까한다.

x175 <-c(rep(1, 4), rep(2,6), rep(3,4), rep(4,4), rep(5,3), rep(6, 2), rep(7,1), rep(8,1))
# or
x175<-c(rep(c(1, 2, 3, 4, 5, 6, 7, 8), c(4, 6, 4, 4, 3, 2, 1, 1)))

# 그래프 그리기
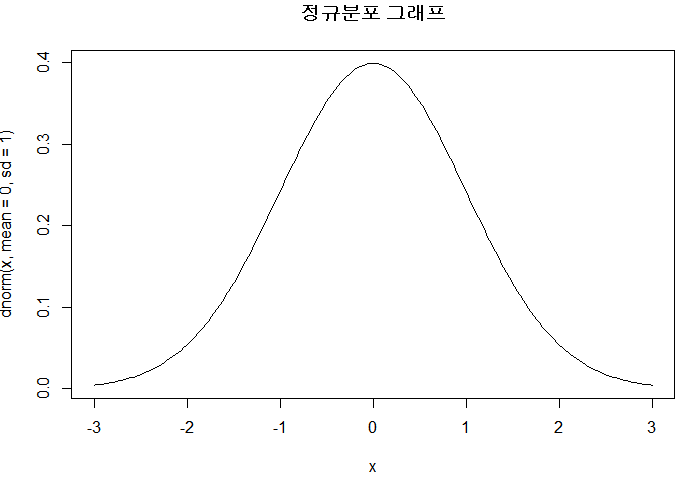
plot(x175, dnorm(x175, mean=mean(x175), sd=sd(x175)), ylab='y', type='l', main="그래프")

여기서 왜도와 첨도를 구하면 아래와 같이 구할 수 있다.

# 왜도(skewness) 구하기
install.packages("fBasics")
library(fBasics)
skewness(x175)

# 첨도(kurtosis) 구하기
kurtosis(x175)